Abstract. We consider the expansion of wave packets governed by the free Schrödinger equation. This seemingly simple task plays an important role in simulations of various quantum experiments, especially in the field of matter-wave interferometry. The initial tight confinement of quantum particles results in a very fast expansion of the wave function at later times which significantly complicates an efficient and precise numerical evaluation. In many practical cases the expansion time is too short for the validity of the stationary phase approximation and too long for an efficient application of Fourier collocation-based methods. We develop an alternative method based on a discretization of the free-particle propagator. This simple approach yields highly accurate results which readily follows from the exceptionally fast convergence of the trapezoidal rule approximation of integrals involving smooth, rapidly decaying functions. We discuss and analyze our approach in detail and demonstrate how to estimate the numerical error in the one-dimensional setting. Furthermore, we show that by exploiting the separability of the Green's function, the numerical effort of the multi-dimensional approximation is considerably reduced. Our method is very fast, highly accurate, and easy to implement on modern hardware.

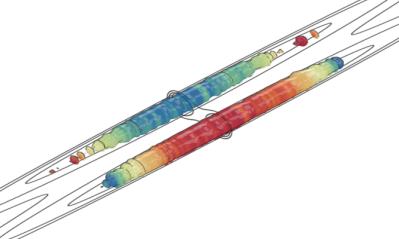
Abstract. We present a detailed analysis of the relaxation dynamics in an extended bosonic Josephson junction. We show that stochastic classical field simulations using Gross-Pitaevskii equations in three spatial dimensions reproduce the main experimental findings of Pigneur et al. [Phys. Rev. Lett. 120, 173601 (2018)]. We give an analytic solution describing the short time evolution through multimode dephasing. For longer times, the observed relaxation to a phase-locked state is caused by nonlinear dynamics beyond the sine-Gordon model, induced by the longitudinal confinement potential and persisting even at zero temperature. Finally, we analyze different experimentally relevant trapping geometries to mitigate these effects. Our results provide the basis for future experimental implementations aiming to study nonlinear and quantum effects of the relaxation in extended bosonic Josephson junctions.

Abstract. Optimal operation and control of (variable-speed) pumped-storage power plants (PSPPs) is essential to meet the growing demands on the dynamics for the stabilization of power distribution grids with an increasing amount of renewable energy sources. Existing work on the control of PSPPs is typically based on rather simplified system models, in particular of the (long) pipeline system. In this article, a nonlinear model predictive control (NMPC) strategy is proposed, which enables fast closed-loop dynamics while keeping all system constraints, including the pressure constraints along the pipeline system. The control strategy is based on a physics-based model, which enables easy parameterization and application to other plant sizes or topologies. To ensure real-time capability of the model predictive control (MPC) strategy, a number of measures are outlined in this article. Finally, the feasibility of the proposed control strategy is demonstrated by detailed simulation studies. An accurate tracking for fast changing desired grid powers as well as a high robustness with respect to parameter uncertainties is demonstrated.

Abstract. Dipolar Bose-Einstein condensates have recently attracted much attention in the world of quantum many body experiments. While the theoretical principles behind these experiments are typically supported by numerical simulations, the application of optimal control algorithms could potentially open up entirely new possibilities. As a proof of concept, we demonstrate that the formation process of a single dipolar droplet state could be dramatically accelerated using advanced concepts of optimal control. More specifically, our optimization is based on a multilevel B-spline method reducing the number of required cost function evaluations and hence significantly reducing the numerical effort. Moreover, our strategy allows to consider box constraints on the control inputs in a concise and efficient way. To further improve the overall efficiency, we show how to evaluate the dipolar interaction potential in the generalized Gross-Pitaevskii equation without sacrificing the spectral convergence rate of the underlying time-splitting spectral method.

Abstract. This paper presents transient numerical simulations of hydraulic systems in engineering applications using the spectral element method (SEM). Along with a detailed description of the underlying numerical method, it is shown that the SEM yields highly accurate numerical approximations at modest computational costs, which is in particular useful for optimization-based control applications. In order to enable fast explicit time stepping methods, the boundary conditions are imposed weakly using a numerically stable upwind discretization. The benefits of the SEM in the area of hydraulic system simulations are demonstrated in various examples including several simulations of strong water hammer effects. Due to its exceptional convergence characteristics, the SEM is particularly well suited to be used in real-time capable control applications. As an example, it is shown that the time evolution of pressure waves in a large scale pumped-storage power plant can be well approximated using a low-dimensional system representation utilizing a minimum number of dynamical states.

Abstract. Pumped‐storage power plants typically feature very long hydraulic pipelines, which can be modeled by a set of partial differential equations. The estimation of the pressure and volumetric flow along the pipes is an important task for the operation of such a plant. Therefore, this work compares different early‐ and late‐lumping–based observer designs for this system. Two late‐lumping observers, ie, a Lyapunov‐based design and an observer using the backstepping design method, are examined. The Lyapunov‐based approach uses a simple boundary correction to stabilize the estimation error dynamics. In contrast, the backstepping‐based approach allows utilizing additional in‐domain correction to obtain a faster rate of convergence. For the implementation of these distributed‐parameter observers, the spectral element method as a flexible and computationally efficient discretization method is introduced. It is shown that, compared with that of the Lyapunov‐based design, the discretization of the backstepping‐based design requires additional spatial grid points for the accurate approximation of its feedback gains. For the early‐lumping approach, the spectral element method is used to approximate the model equations by a system of differential equations. Based on this approximation, an extended Kalman filter is designed. All observer designs are validated and compared for a representative test case.

Abstract. The design of new control strategies for the optimal dynamic operation of pumped-storage power plants requires a realtime-capable mathematical model which describes the pressure and volume flow fluctuations in the pipelines. Classical approaches, like the method of characteristics, result in high-dimensional systems of finite difference equations. This paper describes the application of the spectral element method to the discretization of the underlying partial differential equations. Special attention is put on the implementation of the boundary conditions, using a numerically stable upwind discretization. It is shown by numerical simulation studies that the system dimension can be reduced by at least one order of magnitude by the application of the spectral element method in comparison to the classical method of characteristics.

Abstract. Ultracold gases promise many applications in quantum metrology, simulation and computation. In this context, optimal control theory (OCT) provides a versatile framework for the efficient preparation of complex quantum states. However, due to the high computational cost, OCT of ultracold gases has so far mostly been applied to one-dimensional (1D) problems. Here, we realize computationally efficient OCT of the Gross–Pitaevskii equation (GPE) to manipulate Bose–Einstein condensates in all three spatial dimensions. We study various realistic experimental applications where 1D simulations can only be applied approximately or not at all. Moreover, we provide a stringent mathematical footing for our scheme and carefully study the creation of elementary excitations and their minimization using multiple control parameters. The results are directly applicable to recent experiments and might thus be of immediate use in the ongoing effort to employ the properties of the quantum world for technological applications.

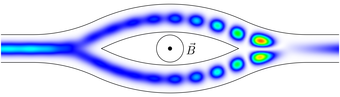
Abstract. Discrete transparent boundary conditions (DTBC) and the Perfectly Matched Layers (PML) method for the realization of open boundary conditions in quantum device simulations are compared, based on the stationary and time-dependent Schrödinger equation. The comparison includes scattering state, wave packet, and transient scattering state simulations in one and two space dimensions. The Schrödinger equation is discretized by a second-order Crank-Nicolson method in case of DTBC. For the discretization with PML, symmetric second-, fourth, and sixth-order spatial approximations as well as Crank-Nicolson and classical Runge-Kutta time-integration methods are employed. In two space dimensions, a ring-shaped quantum waveguide device is simulated in the stationary and transient regime. As an application, a simulation of the Aharonov-Bohm effect in this device is performed, showing the excitation of bound states localized in the ring region. The numerical experiments show that the results obtained from PML are comparable to those obtained using DTBC, while keeping the high numerical efficiency and flexibility as well as the ease of implementation of the former method.

Abstract. Transient simulations of a resonant tunneling diode oscillator are presented. The semiconductor model for the diode consists of a set of time-dependent Schödinger equations coupled to the Poisson equation for the electric potential. The one-dimensional Schrödinger equations are discretized by the finite-difference Crank-Nicolson scheme using memory-type transparent boundary conditions which model the injection of electrons from the reservoirs. This scheme is unconditionally stable and reflection-free at the boundary. An efficient recursive algorithm due to Arnold, Ehrhardt, and Sofronov is used to implement the transparent boundary conditions, enabling simulations which involve a very large number of time steps. Special care has been taken to provide a discretization of the boundary data which is completely compatible with the underlying finite-difference scheme. The transient regime between two stationary states and the self-oscillatory behavior of an oscillator circuit, containing a resonant tunneling diode, is simulated for the first time.

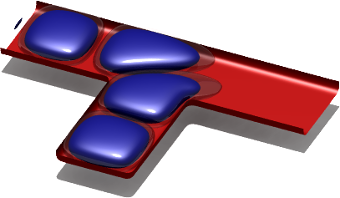
Abstract. The electron flow through quantum waveguides is modeled by the time-dependent Schrödinger equation with absorbing boundary conditions, which are realized by a negative imaginary potential. The Schrödinger equation is discretized by a time-splitting spectral method, and the quantum waveguides are fed by a mono-energetic incoming plane wave pulse. The resulting algorithm is extremely efficient due to the Fast Fourier Transform implementation of the spectral scheme. Numerical convergence rates for a one-dimensional scattering problem are calculated. The transmission rates of a two-dimensional T-stub quantum waveguide and a single-branch coupler are numerically computed. Moreover, the transient behavior of a three-dimensional T-stub waveguide is simulated.